특수 정렬 알고리즘 (1) - 기수정렬

이전까지 우리는 Theta(n의 제곱), Theta(nlogn)의 수행시간이 소요되는 정렬들을 살펴보았는데, 이 정렬들은 (최선/최악)경우에 따라 각각 다른 수행시간이 소요되는 경우도 있었으며, 각 2개의 원소들을 기준으로만 정렬을 했었었다.

그렇다면, 최악의 경우에,

         "Theta(n의 제곱), Theta(nlogn)의 수행시간보다는 더 빠를 수는 없는가?"

이번장에서 알아 볼 기수정렬은 이 최선, 최악의 경우에 관계없는 수행시간과 같은 크기일 경우 자리를 바꾸지않는 안정성이 있는 특징과 "두개의 원소를 비교한다" 보다는 "절대적인 원소를 기준으로 값을 비교한다" 라고 할 수 있다. 이 말은,  최악의 경우에도 최선의 결과와 같은 시간이 소요된다는 것을 의미한다.

그렇다면, 이 기수정렬에 대해 알아보자.

기수정렬은 각 자릿수와 원소의 갯수들만이 수행시간에 영향을 준다.

입력이 모두 k이하의 자릿수인 자연수만을 가진 경우에 사용이 된다.(k는 상수)

각 자릿수만 비교하여 정렬을 원소의 갯수만큼 진행하면 되는데, 위에도 말했듯이 안정적인 정렬을 사용해서 이루어진다. 그림으로 살펴보면 조금 더 쉽게이해가 될 것이다.

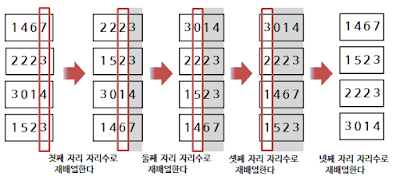
ex) 4개의 자릿수를 갖는 1467, 2223, 3014, 1523의 기수정렬 과정

: 위의 과정에서 안정성 유지하여 정렬한 것

▶ 첫째, 둘째 자릿수 비교 시 2223, 1523 

▶ 넷째 자릿수 비교 시 1467, 1523

기수정렬의 수행시간은 어느 경우에나 Theta(n)의 수행시간이 소요되어야 한다. 어떻게 이러한 수행시간이 가능한가? 

각 자릿수의 범위는 0~9의 사이에 절대적으로 위치할 수 밖에없다. 1000의 자릿수까지 있는 5개의 값이 있다면, 각 자릿수를 0부터 9까지의 숫자 비교를 4번만 하면되지 않겠는가? 물론 안정성 유지를 해야하는 것도 잊지말자.

기수정렬의 알고리즘을 만드는2가지 방법을 살펴보자.

1) 큐를 이용한 방법
  - enqueue() : 큐 삽입 
  - dequeue() : 큐 제거
  - QueueInit() : 큐 초기화
  - QIsEmpty() : 큐 비어있는지 확인.

▶실행결과

2) 2차원 배열을 이용한 방법

▶실행결과