선택 알고리즘

이전에 다음과 같은 정렬들에 대해 알아보았다.

1) 기초적인 정렬(삽입, 선택, 버블정렬)
2) 고급 정렬(병합, 퀵, 힙 정렬)
3) 특수 정렬(기수, 계수 정렬)

이 정렬들의 수행시간을 살펴보면,

최종적인 목표로 최악의 경우 또한 Theta(n)의 수행시간이 소요되는 계수정렬과 기수정렬까지 알아보았는데, 하지만 이 최악의 경우에서도 Theta(n)의 수행시간이 나오기까지 추가적인 메모리가 필요한 약간의 한계성이 있었다.

이러한 추가적인 메모리가 필요한 단점을 보완한 방법으로 선택알고리즘에 대해서 소개하겠다.

선택 알고리즘은 평균적으로 Theta(n)의 수행시간이 소요되며, 추가적인 메로리를 필요로 하지않는다. 그리고 정렬의 목적이 아닌 "어느 특정한 위치의 원소를 찾기 위한것인지"에 맞춘 알고리즘이다.
예를들어, 전체 원소  4, 3, 2, 8, 7중에서 n번째로 작은 값은 어느 원소인지 찾을 수 있으며, 몇 번째로 작은지 찾는 과정에서는 퀵 정렬에서 사용한 partition()을 사용을 통해서 약간의 정렬의 형태를 띄고있다.

선택 알고리즘의 과정은 퀵 정렬시 partition()을 사용하여 기준원소로 전반부와 후반부를 나누는 과정에서 전체원소 중 기준원소는 어느위치에 속하는지 알 수 있었다. 이러한 기준원소의 위치를 알 수 있다는 의미는 "그 값(기준원소)이 전체에서 몇 번째로 작은가 ?" 라는 말과 같은 의미라는 것을 눈치 챌 수있다. 정말로 partition()을 통해 해당원소가 전체에서 몇 번째로 작은지 알 수 있는지 살펴보자

선택 알고리즘 과정 

A = { 4, 3, 2, 8, 7 }에서 2번째로 작은 원소찾기.

 ▶ 과정 (1)

과정(1) partition

: 전반부 3개와 후반부 1개로 나누어졌으며 기준원소(7)보다 큰 값에 대해서는 
 졍렬의 형태를 띈다. 여기서 중요한 것은 배열 인덱스에 초점을 맞춰야 한다.
 전체 0~4의 인덱스 총 5개중에 3번째로 작은 원소의 인덱스값은 3-1인 2가 될 것이다.
 기준원소 7의 인덱스는 partition()수행을 한 결과 3이 되었다. 즉, 우리가 찾는 2보다는
 큰 값으로 기준원소보다 큰 값들에 대해 눈을 떼고 작은 값(전반부)들을 살펴보아야
 한다는 의미이다. 밑의 결과 그림을 보면 쉽게 이해 할 수 있다.

과정(1) selection

: 뒤의 원소 8은 기준원소에 해당하지 않으므로 제외 시켰으며 정렬이 된다.
  그리고 기준원소를 전반부 맨 끝으로 지정

 ▶ 과정 (2)

과정(2) partition

: 전반부 0개와 후반부2개로 나누어 졌으며, 3, 4번째 위치는 이전 과정을 통해서 기준원소  에서 제외된 것을 알 수 있으며 정렬이 된 모습을 띄고있다.

과정(2) selection

: 뒤의 원소 2는 기준원소에 해당하지 않으며, 가장 작은 맨 앞의 위치로 이동한다.
 즉, 전반부는 없으며 후반부를 호출하고 후반부의 맨 끝 4가 기준원소가 된다.


 ▶ 과정 (3)

과정(3) partition

: 후반부 0개와 전반부 1개로 나뉘었으며, 이 말은 찾고자하는 기준원소를 찾았다는 의미라  라고 생각해도 된다. 찾고자 하는 원소는 전반부에 있거나 또는 기준원소가 된다.

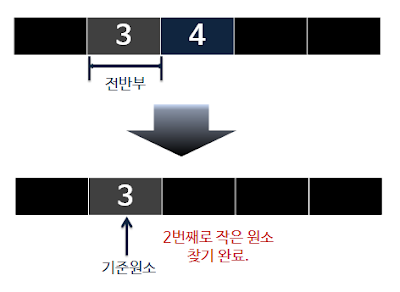과정(3) selection

: 찾기 완료. 후반, 전반이 0이 되거나 기준원소에 해당하지 않을 경우, 비교할 이유가 없으  므로 제외시켰는데 이때 제외시킨 원소들은 정렬이 된 모습을 띈다. 
 (상황에 따라서 정렬이 되지는 않을 경우도 있다는 점을 유의하기)


선택 알고리즘의 수행시간을 살펴보자
1) partition()을 하는 과정에 있어서 원하는 원소를 찾는 것은 Theta(n)의 수행시간이 소요된다. 기준원소와 전체를 비교를 통해서 원하는 값을 찾고 또 기준원소의 자리를 정할 수 있게 된다. 
: 전체와 기준원소의 비교를 하는 시간은 평균 Theta(n)이 소요됨.

2) selection()을 하는 과정은 전체크기에 비례한다. partition()을 통해 기준원소를 알맞은 위치를 찾아서 전반부와 후반부를 각각 호출하는 시간이 소요된다.
: 전체를 전반과 후반부로 나누므로 이들을 호출한느 시간 n이 소요된다. (n은 상수)

위의 1, 2 두 가지 경우를 살펴보면, 계수정렬와 기수정렬때 사용하는 추가적인 메모리 사용없이 평균적인 Theta(n)인 선형시간이 소요될 수 있다. 
하지만, partition()의 경우 퀵 정렬 에서도 살펴 보았듯이 최악의 경우가 존재한다. 바로 전반이 0이되거나 혹은 후반부가 0이되는 기준원소가 한쪽으로만 치우치게 되는경우이다. 
그러므로 다음과 같이 정리할 수 있다.
- 최선의 경우 : Theta(n)
- 평균의 경우 : Theta(n)
- 최악의 경우 : theta(n의 제곱)



선택 알고리즘을 살펴보자



▶실행결과