이번에도 검색 알고리즘과 비슷한 목적인 원하는 원소를 찾아내주는 검색 알고리즘에 대해 소개하겠다.
우리가 만약 원하는 원소를 찾고자할 때, 전체원소가 차례로 나열(정렬)이 되어있다면, 다음과 같이 차례대로 원소를 찾을 것이다.
ex) 순차적 탐색
1) 찾을 원소 : 4
2) 전체원소 1~100에서 그 중 55를 찾고싶다면?
: 위와 같이 54회의 비교를 통해서 찾을 수 있다.
만약에 100의 값을 찾고자 한다면, 99번을 탐색해야하는 과정을 알 수 있을것이다.
이러한 순차적인 탐색은 전체원소의 갯수가 많을경우, 비효율적인 결과를 알 수 있다.
그렇다면, 어떻게하면 이러한 탐색횟수를 줄일 수 있을까? 바로 우리가 지금 알아볼 이진탐색 트리를 알아본다면 쉽게 해결할 수 있다.
먼저, 이진탐색이란?
이진탐색은 전체원소의 중간번째의 원소를 지목해서 찾고자 하는 원소보다 작으면 왼쪽으로 크면 오른쪽으로 탐색이 이루어진다. 쉽게 이해하기위해 다음 이진탐색 그림을 살펴보자.
ex) 이진탐색
A = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 11 }
- 찾을 원소 : 8
과정1) 기준원소: 6
: 찾을 원소 8이 비교할 원소 6보다 큰 7 ~ 11사이에 있다는 것을 확인할 수 있다.
과정2) 기준원소 : 9
: 찾을 원소 8이 비교할 원소 9보다 작은 7 ~ 8 사이에 있다는 것을 확인할 수 있다.
과정3, 4) 기준원소 : 7
: 찾을 원소 8이 비교할 원소 7보다 큰 마지막 남은원소 8이라는 것을 확인할 수 있다.
만약에 여기서 이진탐색이 아닌 순차적인 탐색을 이용했다면, 7회의 과정을 거쳐 탐색을
완료할 수 있었을 것이다. 그리고 원소들을 보면서 "이진탐색은 이미 정렬이 되어있는 상태에서만 사용할 수 있구나" 라고 생각하며 주의하며 이진탐색트리를 살펴보자.
이진탐색트리는 위에서 살펴본 이진탐색을 트리에 얹혀 놓은거라고 생각하면 된다.이전에 힙 정렬에서도 트리에 대해 알아보았는데, 한번 더 살펴보자.
트리는 루트노드(최상위 노드) 부터 최하위의 자식노드(단말노드)까지 (나무의 뿌리처럼 펼쳐진 모양)노드들 간의 연결이 되어있다. 이 하나의 노드에는 (왼쪽자식이 연결될)Left, (오른쪽자식이 연결될)Right 그리고 자신의 (노드의 값)데이터로 다음과 같이 이루어져있다.
ex) 트리에서 사용하는 노드(Node)의 구조
 |
| 값이 2인 노드 |
그리고 이러한 노드들은 최대 두개의 자식들을 가질 수 있으며, 이진탐색트리에서의 노드들은 같은 값을 가질 수 없다. 또한 왼쪽의 자식은 현재 자신의 값보다 작은 값을 가질 수 있고 오른쪽의 자식은 자신보다 큰 값을 가진다.
ex) 트리에서 사용하는 트리의 구조
다시한번 더 이진탐색 트리에서의 노드들을 정의하면 다음과 같다.
1) 노드들은 최대 2개의 자식을 가질 수 있다.
2) 각각의 노드들의 값은 겹치면 안된다. (값이 같으면 X)
3) 노드의 왼쪽자식은 자신보다 작은 값, 오른쪽자식은 자신보다 큰 값을 가져야 한다.
4) 마지막으로 위에 그림에는 없지만, 단말노드(자식이없는, Leaf Node라고도 함)의
왼쪽, 오른쪽자식은 모두 없으므로 NULL을 가리킨다.
왼쪽, 오른쪽자식은 모두 없으므로 NULL을 가리킨다.
이러한 3가지특성을 잘 지키면서 이진탐색트리의 생성, 삭제, 탐색을 살펴보자.
1) 이진탐색 트리의 탐색
1-1) 노드 14의 탐색
: 루트노드부터 Right한번 Left한번의 과정을 거쳐서 값이 14인 노드의 탐색완료
1-2) 노드 7의 탐색
: 노드 7을 탐색하는데 NULL값을 만나서 종료가 된다.
위의 탐색의 과정은 이진탐색트리에서 가장 중요한 역할을 한다. 또한 삭제와 삽입에서도 값을 찾는데 유용하게 이루어지는데, 만약에 탐색을하다가 NULL값을 만나게되면 종료가 된다.
1-1) 노드 14의 탐색
: 루트노드부터 Right한번 Left한번의 과정을 거쳐서 값이 14인 노드의 탐색완료
1-2) 노드 7의 탐색
: 노드 7을 탐색하는데 NULL값을 만나서 종료가 된다.
위의 탐색의 과정은 이진탐색트리에서 가장 중요한 역할을 한다. 또한 삭제와 삽입에서도 값을 찾는데 유용하게 이루어지는데, 만약에 탐색을하다가 NULL값을 만나게되면 종료가 된다.
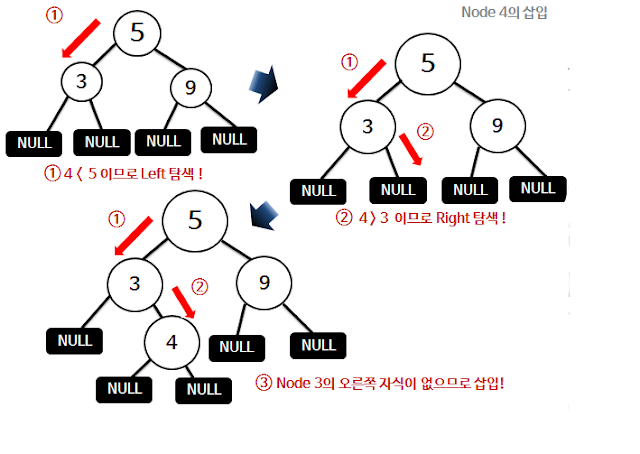
2) 이진탐색 트리의 노드추가
원소 5, 3, 9, 4, 10, 7, 1 차례대로 삽입과정을 알아보자.
2-1) 노드 5 삽입
: 최초의 삽입은 5이므로 Root노드가 된다.
2-2) 노드 3 삽입
: 5의 Left 자식은 없으므로 3은 5의 왼쪽자식이 된다.
2-3) 노드 9 삽입
: 9의 Right 자식은 없으므로 9는 5의 오른쪽자식이 된다.
2-4) 노드 4 삽입
: 3의 Right 자식은 없으므로 4는 3의 오른쪽자식이 된다.
꽤나 복잡해보이지만, 단순한 NULL이 나올때까지 데이터를 삽입하기 위한 탐색이라고 생각하자
2-5) 노드 10 삽입
: 9의 Right 자식은 없으므로 10은 9의 오른쪽자식이 된다.
2-6) 노드 7 삽입
: 9의 Left 자식은 없으므로 7은 9의 왼쪽자식이 된다.
2-7) 노드 1 삽입
: 3의 Left 자식은 없으므로 1은 3의 왼쪽자식이 된다.
2-8) 원소 5, 3, 9, 4, 10, 7, 1 삽입완료.
: 자식이 없는 단말노드들은 NULL을 갖는다.
이제 이진탐색 트리의 삭제에 대하여 알아보자
3) 이진탐색 트리의 노드삭제
이진탐색 트리의 삭제에서는 단순히 노드를 제거하는것에만 신경쓰기보다는 해당 노드를 제거한 뒤에도 트리의 구조를 만족시키는지에 대하여 생각해 볼 필요가 있다. 이러한 이진탐색 트리에서의 삭제는 다음과 같이 세 가지 조건을 항상 염두 해 둔다.
1. 제거할 노드의 자식이 모두 없는 경우(단말노드일 경우)
2. 제거할 노드의 자식이 2개인 경우(자식이 둘 인경우)
3. 제거할 노드의 자식이 하나인 경우(자식은 Left 또는 Right에 위치할 경우)
이러한 이유를 지켜야 트리의 구조가 깨지지 않으므로 항상 유지할 필요가 있다는 것이다.
그림으로 살펴보자.
3-1) 제거할 노드의 자식이 모두 없는 경우(단말노드 일때)
: 제거할 노드가 단말노드일 경우, 단순히 노드만 제거해도 자식들이 없으므로 트리의 규칙이 깨지지 않는다.
3-2) 제거할 노드의 자식이 하나일 경우(자식은 Left, Right 관계없이 같음)
- 원소 22제거
: 22를 제거함.
하지만, 여기서 제거한 노드의 자식들과의 연결또한 끊어지므로, 이것을 유지해야하는 작업이 필요 하다.
- 제거한 노드(22)의 자식들 유지
3-3) 제거할 노드의 자식이 모두 존재할 경우
- 원소 20제거
: 자식이 모두 존재하는 경우, 제거할 노드의 오른쪽 자식에서 가장작은 노드의 값을 제거할 노드에다가 값을 복사해주는데, 그 이유는 제거할 노드의 자식들을 단순히 이어 붙일 수 가 없으며 또한 트리의 규칙을 지키는 복잡한 과정이 필요없이 나아가기에 적합하다.
하지만 여기서 오른쪽노드의 자식들 중 최소값을 붙여준 다음, 최소값의 노드는 제거된다. 왜냐? 같은 트리에 같은노드가 있을 수 없다. 그리고 최소값의 노드 또한 트리의 규칙에 맞게 제거가 되어야 한다.
- 최소값 제거 후 자식들을 트리의 구조에 맞게 정리
이진탐색트리의 수행시간
이진탐색트리의 수행시간은 "데이터의 분포에 따라서 달라진다" 라고 할 수 있다.
이해하기 힘들겠지만, 지금까지 위에서 살펴본 노드들이 어떠한 형태로 트리에 위치했는지 살펴보진 않았을 것이다. 데이터의 탐색을 하기 위해서는 항상 Root의 노드부터 차례로 크기 비교를통해서 탐색이 되었다. 이말은 트리의 노드들이 한쪽으로만 치우쳐져 있다면, 크기 비교하는것에 의미를 두지않고 한쪽으로만 탐색해야한다는 굉장히 비효율적인 탐색이 되는것이다.
그림으로 살펴보자.
- 트리의 노드들이 골고루 분포되어있는 경우
:위에서 살펴보듯이 트리에 데이터가 골고루 분포가 되어 있다면, 3회에 걸쳐 찾을 수 있다.
이말은 다르게 말하면 이진탐색트리의 수행은 Theta(log n)의 시간이 소요된다.
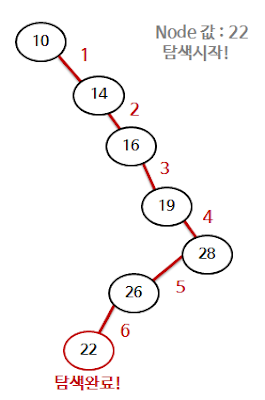
- 트리의 노드들이 치우쳐져 있는 경우
: 이처럼 트리에서 한쪽으로만 치우쳐져있는 노드들의 구조는 최악의 경우라고 할 수 있다. 이처럼 최악의 경우에서는 전체노드들의 갯수, Theta( N )의 수행시간이 소요된다.
최종적으로 정리하면 다음과 같다.
- 최선의 탐색 수행시간 : Theta( n )
- 최악의 탐색 수행시간 : Theta( log n )
- 평균적인 탐색 수행시간 : Theta( log n)
이진탐색 트리의 알고리즘은
- BinarySearchTree.h
- BinarySearchTree.c
- BinarySearchTreeMain.c
▶실행결과






















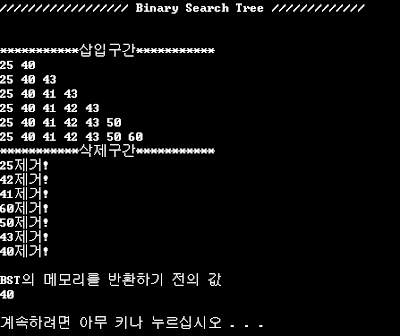



코드 수정(1)
답글삭제BSTNode * BST_RemoveNode(BSTNode * Tree, BSTNode * Parent, Data data)에서
제거될 노드의 자식이 2명인 조건에서,
if (Tree->Left != NULL && Tree->Right != NULL)
{
BSTNode * delNode = BST_SearchMinNode(Tree->Right);
Removed = BST_RemoveNode(Tree, NULL, delNode->data);
Tree->data = delNode->data;
}
으로 수정됨. 이전 코드에서는 노드의 최소값을 덮어쓰기했으나, 실제로 제거되지않는 오류가 존재했었음